The Kempe Tree: A Simple Data Structure for Supporting Range Updates or Queries

Introduction

This post describes two variations on tree structure that I've used in some programming problems for solving variations of the range query/update problem. I haven't seen anyone else use it before, so for the moment I'm going to call it the Kempe tree, named after my great-grandfather who was also named Richard Kempe.

Suppose we are given a list of data \( a_0, a_1, \ldots, a_{n-1} \). In general terms, range update data structure supports the following type of operation: \[ update( i, j, x ): a_k \leftarrow x \text{ for all } k \in \{ i, i+1, \ldots, j \} \] Similarly, a range query data structure supports the following type of operation: \[ query( i, j ) = f( a_i, a_{i+1}, \ldots, a_{j} ) \] (Here \( f \) is taken to be some function we can aggregate over a large number of values, like \( \min \), \( + \), etc....) Both of these operations are expected to be reasonably fast, usually taking at most \( O( n ) \) steps.

As an example, segment trees and Fenwick trees (or binary-indexed trees) are range query data structures. Segment trees with lazy propagation support both range queries and range updates.

The Kempe tree is a data structure that supports either fast range updates and single-element queries, or fast range queries and single-element updates, but not both simultaneously. (Okay, fine, it can support both, provided one is \( O( \log^2 n ) \). But more on that later.) Why, then, should I use a Kempe tree, you ask? The main reason is that it uses numerical tricks to make it easier to code, the same reason why the Fenwick tree is sometimes used instead of the segment tree. (This also means that, for all intents and purposes, Kempe trees will never be used outside of competition programming.)

Range Traversals

The Kempe tree, like the Fenwick tree, is an array-based tree. Suppose we have \( n \) data entries, a[0], a[1], ..., a[n-1]; then we require an array of size \( N + n \), where \( N \) is the smallest power of \( 2 \) that is \( \geq n \). Let tree[i] denote this array. The entries of tree[i] are allocated as follows:

• Elements a[0], a[1], ..., a[n-1] are stored in entries tree[N], tree[N+1], ..., tree[N+n-1], respectively.
• The parent node for any entry tree[i] is tree[i/2].
• Likewise, a non-leaf node tree[i] has children tree[2*i] and tree[2*i+1].
• The root of the tree is tree[1].

See the following image for a description of the mapping. Numbers in the tree nodes denote position in the array tree[i].

We say a tree node governs the array entries that are its descendants. For some range a[i], a[i+1], ..., a[j], the following algorithm finds the minimal set of tree nodes tree[x[0]], tree[x[1]], ..., tree[x[m-1]] that govern a[i], a[i+1], ..., a[j]:

vector find_governing_nodes( int i, int j )
{
  vector ans;
  i += N, j += N;
  while( i <= j )
  {
    if( i % 2 == 1 ) ans.push_back( i );
    if( j % 2 == 0 ) ans.push_back( j );
    i = ( i + 1 ) / 2;
    j = ( j - 1 ) / 2;
  }
  return ans;
}

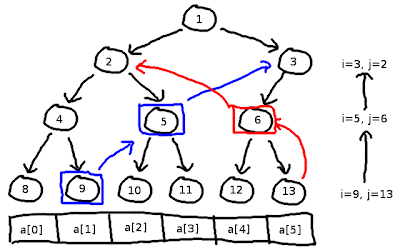
A sketch of the proof for the correctness of the algorithm is the following. We start with i and j at the ends of the interval we are interested in. We process the interval by moving i and j up the tree, and by 'pulling' them together. If moving either i or j shrinks the interval during the next step, then we add them to the list of governing nodes. The following image illustrates the process in action:

1. We wish to query the range \( [1, 5] \). i and j are initialised to 9 and 13, respectively.
2. Since 9 would jump out of its subtree during the next move, we add 9 to the list of governing nodes.
3. We move i to 5 and j to 6. Both i and j will jump out of their respective ranges during the next move, so we add both 5 and 6 to the list of governing nodes.
4. i gets moved to 3, and j to 2. This is an invalid range, so we break and return the list [9, 5, 6].

Range Queries and Singleton Updates

We now present an example of a tree structure that can handle updates to single elements and range queries. The function we will try to query is the sum function.

// define MAX to be some really big number

int tree[MAX], N;

// initialises a tree for n data entries
int init( int n )
{
  N = 1;
  while( N < n ) N *= 2;
  for( int i = 1; i < N + n; i++ ) tree[i] = 0;
}

// compute the product a[i] + a[i+1] + ... + a[j]
int range_sum( int i, int j )
{
  int ans = 1;
  for( i += N, j += N; i <= j; i = ( i + 1 ) / 2, j = ( j - 1 ) / 2 )
  {
    if( i % 2 == 1 ) ans += tree[i];
    if( j % 2 == 0 ) ans += tree[j];
  }
  return ans;
}

// set a[i] = val
void update( int i, int val )
{
  int diff = val - tree[i+N];
  for( int j = i + N; j; j /= 2 ) tree[j] += diff;
}

Range Updates and Singleton Queries

The following example will allow us to increment a range, while allowing us to query the result on a singleton value.

// define MAX to be a really big number

int tree[MAX], N;

// initialises a tree for n data entries
int init( int n )
{
  N = 1;
  while( N < n ) N *= 2;
  for( int i = 1; i < N + n; i++ ) tree[i] = 0;
}

// increments a[k] by val for all k between i and j, inclusive
void range_increment( int i, int j, int val )
{
  for( i += N, j += N; i <= j; i = ( i + 1 ) / 2, j = ( j - 1 ) / 2 )
  {
    if( i % 2 == 1 ) tree[i] += val;
    if( j % 2 == 0 ) tree[j] += val;
  }
}

// compute a[i]
int query( int i )
{
  int ans = 0;
  for( int j = i + N; j; j /= 2 ) ans += tree[j];
  return ans;
}

Final Remarks

We can easily extend the tree to support many types of functions, such as the product function, min, max, set union, set intersection, and so forth.

Unfortunately, under the current scheme, the tree cannot simultaneously support range updates and queries. There is a way to support both operations, provided that one operation takes \( O( \log n ) \) and the other takes \( O( \log^2 n ) \). (The proof of this is left to the reader.) Thus, Kempe trees do not provide as much functionality as segment trees, but are generally somewhat easier to code.